标签： C++

基本知识

类型的函数

我们都知道模板可以接受类型作为「参数」。同样地我们也可以有「返回值」，从而构造类型的函数。基本的范式是：

template<class T>
struct Computed {
  using type = T;
}

这就构造了一个名为 Computed 的，接收一个类型参数，返回这个类型本身的函数，用法如 Computed<float>::type，这个类型应当还是 `float`。
为什么要包一层 struct？这是因为 C++ 不支持对 using 的特化。这样的代码是不行的：

template <class T>
using computed<T> = T;

template<>
using computed<int> = double;

至于为什么不支持，我没有了解。

特化

什么是特化？你可以理解为模式匹配，就像 Haskell 中的写法一样。

template<class T>
struct Computed {
  using type = T;
}

template<>
struct Computed<int> {
  using type = double;
}

这样当你调用 Computed<bool>::type 时，得到的结果是 bool，而调用Computed<int>::type得到的结果却是double。当然这种匹配是遵循一定规则的，比如更「具体」的特化优先匹配，这跟 Haskell 谁在前谁先试着匹配不太一样。在 Haskell 中就好比：

data Type = Bool | Double | Int

computed :: Type -> Type
computed Int = Double
computed t = t

实际上有了这层对应，如果你知道怎么在 Haskell 中实现 Peano 数，那么 C++ 中的实现基本就是无脑翻译了。如果你不知道怎么在 Haskell 中实现 Peano 数，那你知道 Peano 数是什么，也能大差不差知道答案了。

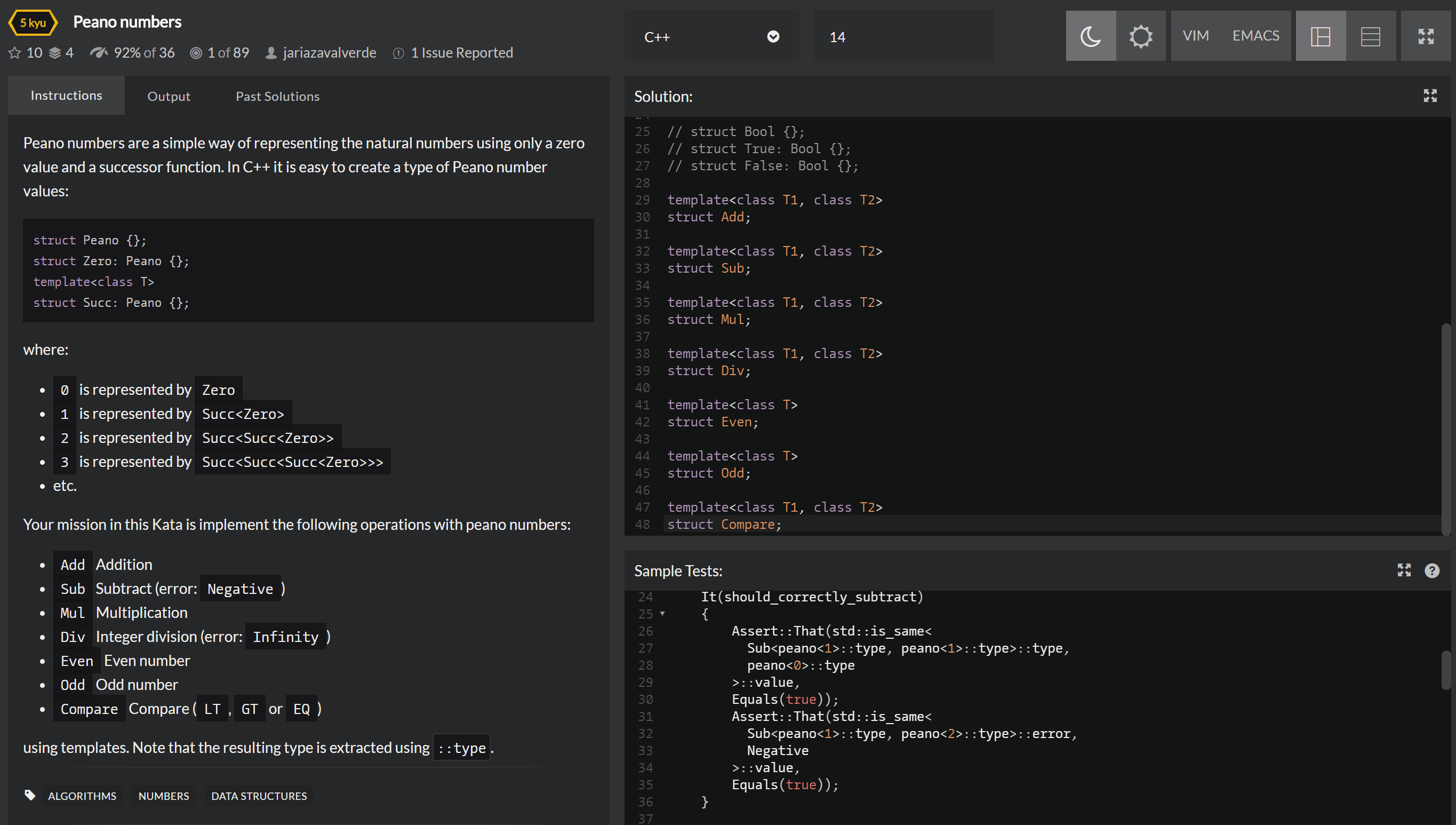
Peano 数

Peano 数是什么？Peano 数是归纳定义的自然数，准确地说应该是一个表现形如直觉中「自然数」的公理系统，也就是「自然数」的形式化。这个系统里只有两个符号，Zero——表示 0，以及 Succ——表示后继。那么 1 就是 Succ<Zero>，2 就是 Succ<Succ<Zero>>，以此类推（归纳，其实就是「以此类推」的形式化）。
我们可以在 C++ 中如此表述：

struct Peano {};
struct Zero: Peano {};
template<class T>
struct Succ: Peano {};

那么加法又是什么呢？从例子出发，我们需要定义一个两个类型参数的模板：

template<class T1, class T2>
struct Add {
  using type = ???;
}

满足直觉中的运算规律，比如 2+1=3，翻译成 C++ 就是 Add<Succ<Succ<Zero>>, Succ<Zero>>::type = Succ<Succ<Succ<Zero>>>。当然类型之间没有等于号，准确地说应该用 std::is_same<T1, T2>，这其实也是通过特化实现的，比如（示意，非官方实现）：

template<class T, class U>
struct is_same {
  static constexpr bool value = false;
};
 
template<class T>
struct is_same<T, T> {
  static constexpr bool value = true;
};

那么如何定义加法呢？对于有限的元素，我们当然可以为每一个实例做特化，比如：

template<>
struct Add<Succ<Succ<Zero>>, Succ<Zero>> {
  using type = Succ<Succ<Succ<Zero>>>;
}

也就是打表。C++ 编译器的模板深度一般都是有限的，所以这理论上是可以在实际操作中覆盖所有用例的。但是这明显太傻了。其实加法的定义只需要两条规则就可以覆盖：0 + b = b, (Succ a) + b = Succ (a + b)。翻译成 C++ 就是：

template<class T1, class T2>
struct Add;

template<class T>
struct Add<Zero, T> {
  using type = T;
};

template<class T1, class T2>
struct Add<Succ<T1>, T2> {
  using type = Succ<typename Add<T1, T2>::type>
};

注意那个 typename，gcc 并不知道后面那个 ::type 成员是类型还是变量，所以需要 typename关键字的提示。
这就算写完了，你可以测试看看，是不是满足 std::is_same<Add<Succ<Succ<Zero>>, Succ<Zero>>::type, Succ<Succ<Succ<Zero>>>>::value == true（需要 <type_traits> 头文件，或者上面自己写的那个模板（那就不用加 std::）。这么嵌套着写 Succ 太繁琐了，也不方便看，你可以简单地写一个模板来从整数生成类型：

template<int v>
struct peano {
  using type = Succ<typename peano<v - 1>::type>;
};

template<>
struct peano<0> {
  using type = Zero;
};

然后就可以去验证 Add<<peano<2>::type, peano<1>::type>::type 是不是等于 peano<3>::type 了。
至于加减乘除的其他运算，比较啊奇偶性啊其他的函数，只要你懂得了加法，恐怕就不难了。

练习：

在 Peano numbers | Codewars 完成加减乘除、奇偶性和比较大小的撰写，并通过测试。

后记

当然我们还可以进一步「证明」我们印象中的结论，比如加法是满足交换律的，加法和乘法是满足分配率的，等等。这就是后话了。