Fundamentals
Function on Types
We all know that C++ templates can receive types as “parameters”. In the same spirit we could can “return values”s, so that we can form a function. The basic paradigm is the following:
template<class T>
struct Computed {
using type = T;
}In this way we constructed a type level function named Computed, with one parameter and result the parameter itself. We use the function as Computed<float>::type, the result being float itself.
Why an extra structwrapper instead of directly defining the “function”? That’s because partialization on using is not allowed. Such codes are invalid:
template <class T> using computed<T> = T; template<> using computed<int> = double;
Partialization
template<class T>
struct Computed {
using type = T;
}
template<>
struct Computed<int> {
using type = double;
}Computed<bool>::type would become bool, while Computed<int>::type would (specially) be double. Certainly, there are a set of rules for the matching process. E.g. the most “specific” case gets matched first. This is somewhat from Haskell, where the first-defined case comes first. The equivalent code in Haskell is:data Type = Bool | Double | Int computed :: Type -> Type computed Int = Double computed t = t
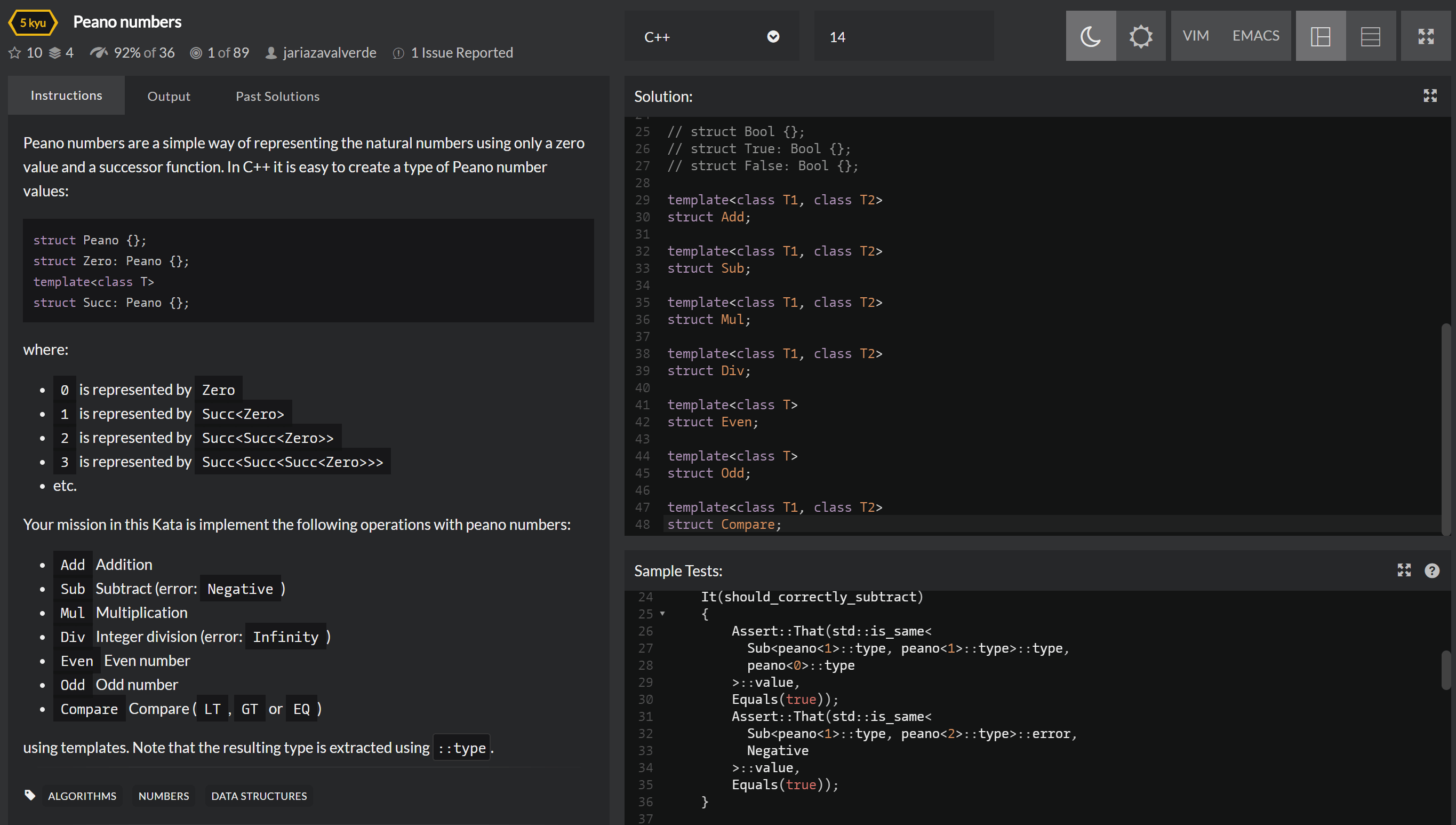
Peano numbers
Zero for 0, and a Succ for the successive. Thus 1 would be Succ<Zero>, 2 would be Succ<Succ<Zero>>, and so on. This is but the heuristic demonstration of “induction”.struct Peano {};
struct Zero: Peano {};
template<class T>
struct Succ: Peano {};template<class T1, class T2>
struct Add {
using type = ???;
}2+1=3, or Add<Succ<Succ<Zero>>, Succ<Zero>>::type = Succ<Succ<Succ<Zero>>>. Certainly the latter expression is not valid C++, since there is no equality operator for types. Instead, we should use the std::is_same<T1, T2> function, which is predefined in <type_traits>. Or you can implement it yourself, again using partialization. This is a possible implementation:template<class T, class U>
struct is_same {
static constexpr bool value = false;
};
template<class T>
struct is_same<T, T> {
static constexpr bool value = true;
};template<>
struct Add<Succ<Succ<Zero>>, Succ<Zero>> {
using type = Succ<Succ<Succ<Zero>>>;
}0 + b = b, (Succ a) + b = Succ (a + b). In C++ they are:template<class T1, class T2>
struct Add;
template<class T>
struct Add<Zero, T> {
using type = T;
};
template<class T1, class T2>
struct Add<Succ<T1>, T2> {
using type = Succ<typename Add<T1, T2>::type>
};typename — the compiler doesn’t know whether the ::type is a member type or a member variable, so we need this keyword as a hint.std::is_same<Add<Succ<Succ<Zero>>, Succ<Zero>>::type, Succ<Succ<Succ<Zero>>>>::value == true or so. Such nesting of Succ is somewhat hard to read, so you can simply write a template to generate Peano types from integers:template<int v>
struct peano {
using type = Succ<typename peano<v - 1>::type>;
};
template<>
struct peano<0> {
using type = Zero;
};Then you can simplify it to Add<peano<2>::type, peano<1>::type>::type and peano<3>::type. The other opeartions like subtraction, multiplication and division can be similarly implemented, which are left as exercises.
Exercises:
Afterwords
We can further “prove” the assertions in our intuition, such addition is commutative, multiplication is distributive over addition, and so on. We may talk about this later.



huge 數學歸納需要專門去學習麼
我觉得最好去学一学实分析开头定义自然数的部分,自然就懂了。
这个配色看着很费眼睛诶,背景和字体的颜色反差太大了。